ESERCIZIO INTRODUTTIVO ALLO STUDIO DI FUNZIONE

Della funzione seguente definire il dominio, il segno, le eventuali intersezioni con gli assi, la parità e, nell'intervallo , verificare se la funzione risulta crescente o decrescente.

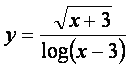
DOMINIO

Nella funzione frazionaria sono presenti: a numeratore una radice quadrata avente come argomento un polinomio e a denominatore un logaritmo in base dieci (maggiore di uno) avente come argomento un polinomio.
Il dominio di esistenza della finzione sarà quindi dato dal sistema tra:

• l'esistenza dell'argomento della radice

• l'esistenza dell'argomento del denominatore e

• il denominatore diverso da zero

Numeratore

Denominatore

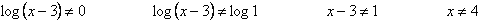
mettiamo il tutto su un grafico

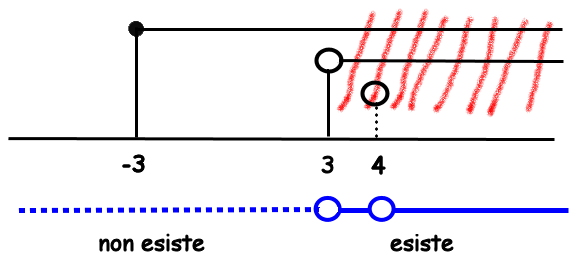
ed osserviamo che il dominio è

SEGNO

poniamo la funzione maggiore di zero

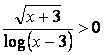
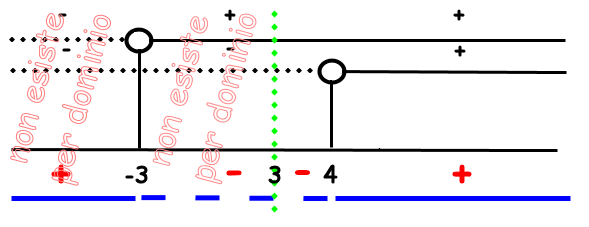
dal grafico possiamo vedere che c'è una zona del piano dove la funzione non esiste per il dominio, una zona nella quale assume valori negativi (da 3 a 4) ed una zona in cui assume valori positivi (da 4 a + infinito) e si osserva anche (vedi dominio) che per x = 4 la funzione diverge

INTERSEZIONI CON GLI ASSI

La funzione interseca l'asse x quando y = 0. Ciò avverrebbe quando il numeratore si annulla ovvero per x=-3, ma questo non può accadere perché -3 appartiene ai valori di x per cui la funzione non è definita (vedi dominio) per cui la finzione non interseca mai l'asse x.
La funzione interseca l'asse y quando la x = 0. Ciò non è possibile per il dominio e quindi non interseca mai neppure l'asse y.

PARITA'

Sostituendo –x nella funzione si osserva che non è né pari né dispari.

CRESCENTE – DECRESCENTE

Andiamo ad analizzare l'andamento della funzione nell'intervallo proposto .Andiamo quindi a sostituire due valori 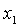e 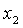da noi opportunamente scelti con 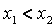. Ad esempio prendiamo in considerazion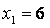e e 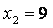. Calcoliamo i valori della funzione in corrispondenza dei due valori

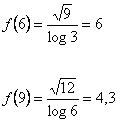
Essendo 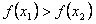allora la funzione, nell'intervallo proposto, risulta decrescente

in effetti il grafico della funzione è