DISEQUAZIONE DI GRADO SUPERIORE AL PRIMO

riconducibile a disequazione di primo grado

Consideriamo il seguente testo

Porto tutti i termini al primo membro

trasformo l'espressione in un'unica frazione facendo il mcm

moltiplico e semplifico i termini simili, se presenti

scompongo il numeratore in modo da ottenere solo termini di primo grado

soluzione

essendo il numeratore composto da due polinomi di primo grado, li analizzo singolarmente

N)

1° Numeratore

2° Numeratore

facciamo il grafico relativo alle soluzioni del numeratore (N)

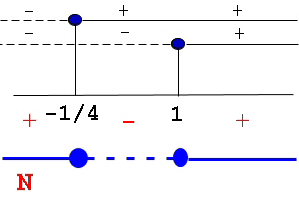
riempiendo il pallino in quanto il simbolo della disequazione è maggiore-uguale a zero

D)

facciamo il grafico relativo al denominatore (D)

D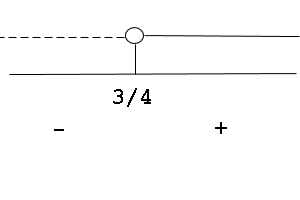

in questo caso il pallino rimane vuoto in quanto il valore 3/4 renderebbe nullo il denominatore e quindi impossibile l'espressione (pallino vuoto = valore escluso)

ora consideriamo insieme la soluzione relativa al numeratore e quella relativa al denominatore e facciamo il prodotto dei segni

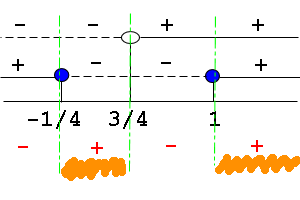
Dovendo essere la soluzione maggiore uguale a zero si prendono in considerazione gli intervalli con valore + (> 0) evidenziati in arancione

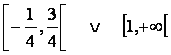
Quindi la soluzione è data dall'insieme dei valori dell'intervallo da -1/4 (compreso) a 3/4 (escluso) unito ai valori dell'intervallo da 1 (compreso) a + infinito (escluso)

in simboli