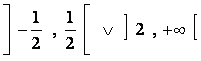DISEQUAZIONE DI GRADO SUPERIORE AL PRIMO

riconducibile a disequazione di primo grado

Consideriamo il seguente testo

Da una prima occhiata mi accorgo che è una disequazione intera, di grado superiore al primo, con un termine di primo grado che moltiplica un termine di secondo grado.
Passo quindi a scomporre il termine di secondo grado per ridurre la disequazione a prodotti di polinomi di primo grado

ora posso risolvere la disequazione analizzando i termini di primo grado singolarmente

soluzione

1° 

essendo la x negativa moltiplico ambo i menbri della disequazione per -1 e cambio il verso della disequazione

2° 

3° 

moltiplicando per -1 e cambiando il verso della disequazione si ottiene

mettiamo insieme le soluzioni in un unico grafico

osserviamo che i pallini sono vuoti in quanto il simbolo della disequazione è solo maggiore(pallino vuoto = valore escluso )

Facciamo il prodotto dei segni.

Dovendo essere la soluzione maggiore di zero si prendono in considerazione gli intervalli con valore + (> 0) evidenziati in giallo

Quindi la soluzione è data dall'insieme dei valori dell'intervallo da -1/2 (escluso) a 1/2 (escluso) unito ai valori dell'intervallo da 2 (escluso) a + infinito (escluso)

in simboli