DISEQUAZIONE DI GRADO SUPERIORE AL PRIMO
riconducibile a disequazione di primo grado
Consideriamo il seguente testo
![]()
Da una prima occhiata mi accorgo che è una disequazione intera, di grado superiore al primo, con un termine di primo grado che moltiplica un termine di secondo grado.
Osservo che il termine di secondo grado è già scomposto.
ora posso risolvere la disequazione analizzando i termini di primo grado singolarmente
soluzione
essendo x2 scomponibile in x per x possiamo procedere così
1° ![]()
2° ![]()
In realtà posso già affermare che il termine x2 mi darà sempre soluzioni positive perché ![]() è sempre
è sempre ![]()
3° ![]()
![]()
mettiamo insieme le soluzioni in un unico grafico
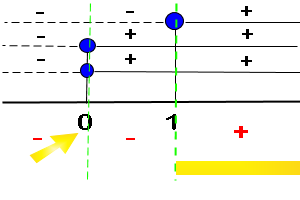
osserviamo che i pallini sono pieni in quanto il simbolo della disequazione è maggiore-uguale(pallino vuoto = valore escluso invece pallino pieno=valore compreso)
Facciamo il prodotto dei segni.
Dovendo essere la soluzione maggiore-uguale di zero si prende in considerazione l'intervallo con valore + (> 0) evidenziato in giallo e il valore 0 (zero) perché:
- lo 0 soddisfa la disequazione
- lo 0 è positivo
Quindi la soluzione è data dall'insieme dei valori: 0 unito ai valori dell'intervallo da 1 (incluso) a + infinito (escluso)
in simboli
![]()
