EQUAZIONE PARAMETRICA FRATTA

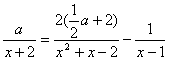
Questa è un'equazione parametrica fratta perché al denominatore sono presenti termini con la x

Per prima cosa abbiamo svolto il prodotto del secondo numeratore eliminando così la parentesi a numeratore. Successivamente abbiamo scomposto il secondo denominatore (trinomio notevole) in modo da avere, a denominatore, tutti termini primi per poter calcolare il mcm.

Troviamo il Campo di Esistenza

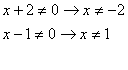
Abbiamo trovato il m.c.m e l'abbiamo diviso per i denominatori e moltiplicato per i numeratori.

Essendo i denominatori uguali ed avendo individuato il CE, li abbiamo semplificati riscrivendo così l'equazione semplificata.

Per avvicinarci alla soluzione abbiamo portato i termini con l'incognita a sinistra e i valori senza incognita a destra.

L'incognita x è in comune nei termini a sinistra, pertanto l'abbiamo raccolta così come abbiamo raccolto il 2 a destra dell'equazione (2a + 2).

Abbiamo cosi trovato la soluzione dell'equazione. Inoltre in quest'ultimo passaggio dobbiamo anche semplificare gli elementi uguali,per ottenere come risultato x=2

Discussione:

una volta osservato che la semplificazione del denominatore è possibile se

il risultato sarà

per eq. Indeterminata

per eq. impossibile (CE)

per eq.impossibile (CE)

infine per l'equazione risulta determinata ed ha per risultato