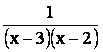ESPRESSIONE FRAZIONARIA

Prendiamo in considerazione la seguente espressione frazionaria

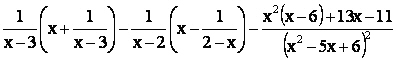
ed iniziamo osservandla nella sua globalità. Iniziamo ad individuare alcune caratteristiche su cui successivamente interverremo:
1_il primo termine è un prodotto tra una frazione e il contenuto di una parentesi; nella parentesi il denominatore è scomposto e si deve fare solo il mcm
2_ il secondo termine è un prodotto tra una frazione e il contenuto di una parentesi; osservo che il denominatore all’interno della parentesi è scomposto ed è uguale ma con segni opposti al denominatore fuori dalla parentesi. Quindi un’azione da prevedere sarà quella di cambiare il segno del denominatore nella parentesi per renderlo uguale a quello fuori dalla parentesi
3_ il terzo termine è una frazione con il numeratore che andrà svolto e il denominatore composto da un trinomio di secondo grado, al quadrato, che sarà utile scomporre (trinomio caratteristico).
Iniziamo con il sommare i termini nelle parentesi, cambiare il segno al denominatore osservato prima e a scomporre il denominatore del terzo termine.

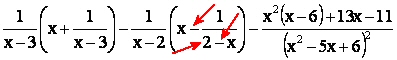
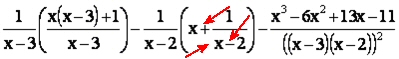
Ora passiamo sa individuare il CE ovvero i valori che annullano i denominatori

CE: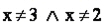

moltiplichiamo

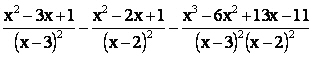
facciamo il mcm tra i tre termini dell'espressione e sommiamo le tre frazioni

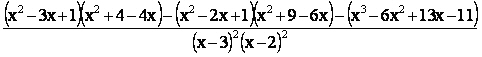
dopo aver cambiato il segno tra parentesi e semplificato otteniamo

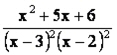
scomponiamo il numeratore e semplifichiamo

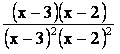
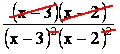
ottenendo quindi