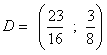PROBLEMA SULLA RETTA 1

testo del problema

Il triangolo isoscele ABC ha il vertice C sulla retta e gli estremi della base nei punti e . Determinare le coordinate del circocentro D.

circocentro: punto di incontro degli assi dei lati ovvero centro della circonferenza circoscritta

Innanzi tutto rappresentiamo graficamente la retta e i punti A, B, C i lati AB e BC e in modo da visualizzare i dati e trarne così elementi utili alla soluzione

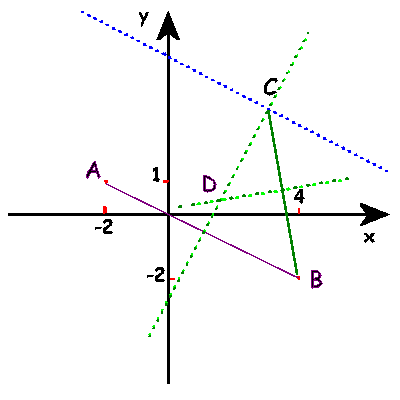
Data la definizione di circocentro per trovare il punto richiesto occorre avere l'equazione di almeno due assi (di due lati) che messi a sistema daranno il punto stesso.
Per trovare l'equazione di un asse dobbiamo:

• trovare l'equazione della retta su cui giace il lato (ovvero l'equazione della retta passante per due vertici) per poterne individuare il coefficiente angolare
• trovare il punto medio del corrispondente lato

a questo punto l'asse è dato dall'equazione della retta passante per il punto medio e coefficiente angolare dato dall'opposto dell'inverso (retta perpendicolare) di quello della retta su cui giace il lato.

Per trovare il vertice del triangolo, essendo questo isoscele, porremo la distanza AC uguale a BC (lati congruenti). Così facendo troveremo l'equazione dell'asse relativo la lato AB

(ricordiamo che l'asse è il luogo dei punti del piano equidistanti dagli estremi del segmento ovvero il luogo dove è sempre vero che AB=BC)

successibamente lo porremo a sistema con la retta data trovando così il vertice C cercato.

Trasformiamo l'equazione in forma esplicita , quindi

ricordando che poniamo

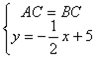
sviluppati i due argomenti, elevati al quadrato i due termini dell'uguaglianza, semplificati i termini simili si ottiene

asse del lato AB

quindi

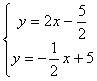
che risolto darà le coordinate del vertice

ora ci calcoliamo l'asse BC
punto medio M di BC : ,

punto medio: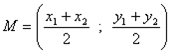

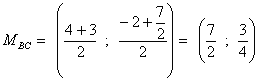
retta passante per due punti:

retta per BC: 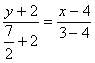semplificando si ottiene: con

l'equazione dell'asse di BC passante per 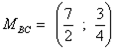e con coefficiente angolare sarà

che semplificata ed esplicitata diventa (asse del lato BC)

ponendo a sistema le equazioni dei due assi (asse di AB e asse di BC) otterremo le coordinate del circocentro

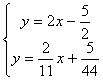
risolto, avremo le coordinate cercate