PROBLEMA SULLA RETTA 2

testo del problema

trovare le coordinate del punto P appartenente alla retta e distante dal punto

Innanzi tutto rappresentiamo graficamente la retta e il punto D in modo da visualizzare i dati e trarne così elementi utili alla soluzione

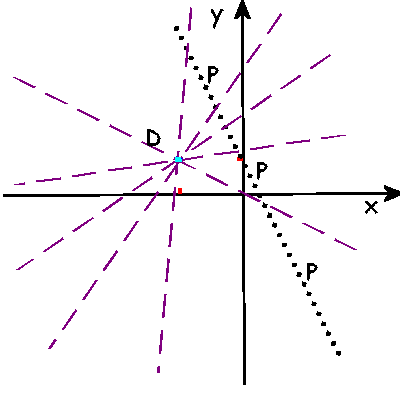
Osservando il grafico possiamo prevedere che il risultato sarà dato da due punti P1 e P2 in quanto simmetrici, sulla retta, rispetto a D

PRIMA IPOTESI RISOLUTIVA

Osservando attentamente il grafico possiamo immaginare che per il punto D passino infinite rette (fascio proprio), quindi i punti cercati sono quelli che nascono dall'intersezione tra due di queste rette con la retta data e distano dal punto D di

conseguentemente prima scriviamo l'equazione del fascio di rette passante per D

   eq. generica passante per un punto

sostituendo il punto abbiamo e svolgendo otteniamo

ora poniamo a sistema l'equazione data con quella del fascio di rette

per trovare le coordinate x e y del generico punto ottenuto dall'intersezione della retta data con tutte le rette del fascio; queste coordinate dipenderanno quindi dal coefficiente angolare (m) di ogni singola retta del fascio.
Fatte le sostituzioni e le semplificazioni otteniamo dopo aver posto

  e 

Ora abbiamo:
il punto e il generico punto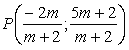

Per trovare l'incognita m abbiamo bisogno di una condizione: la condizione cercata è che la distanza tra i punti deve essere uguale a

imponiamo quindi che la distanza tra i due punti sia

partendo da e sostituendo otteniamo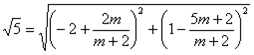

dopo aver svolto i quadrati sotto radice, semplificato, elevato al quadrato i due membri dell'uguaglianza per togliere le radici, otteniamo

risolvendo dopo aver posto otteniamo un'equazione di secondo grado

da cui otteniamo e che sostituiti in P daranno

e i punti cercati

§ -- § -- §

SECONDA IPOTESI RISOLUTIVA

Un altro approccio potrebbe essere quello di immaginare tutti i punti distanti dal punto D che intersecano la retta data 

Con un po' di fantasia possiamo vedere che l'insieme di tutti i punti equidistanti da D formano, nello spazio, una sfera e questa sfera interseca la retta in due punti; più precisamente questi due punti appartengono, nel piano, ad una circonferenza (CIRCONFERENZA: luogo dei punti del piano equidistanti da un punto chiamato centro).

Quindi possiamo procedere nel seguente modo:
imponiamo che la distanza tra un generico punto e sia uguale a

sviluppato l'argomento della radice ed elevati al quadrato i due termini dell'uguaglianza otteniamo una equazione di secondo grado (eq. circonferenza)

(eq. di una circonferenza)

 cercheremo quindi le coordinate dei punti in cui questa curva interseca la retta data ponendoli a sistema

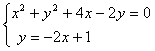
sostituendo e semplificando otterremo una equazione di secondo grado

che risolta ci darà i due valori x dei due punti e

sostituendo nell'eq. della retta i due valori di x otterremo i corrispondenti valori di y

e

per cui i punti cercati sono e