RAPPRESENTAZIONE E OPERAZIONI CON INSIEMI

Sia:
A = , B = , C = ,
U = semplificare la seguente espressione , rappresentarne il risultato con i diagrammi di Venn e definire in base ai valori degli insiemi A, B e C, l'insieme D risultante (in forma estensiva):

A =

Sapendo che l’elemento x, è tale che indica tutti quei numeri naturali maggiori di 10 ma minori di 26 (compreso quest’ultimo); inoltre l’elemento x in questione indica i numeri pari.
Quindi il risultato della semplificazione dell’espressione in questione sarà:

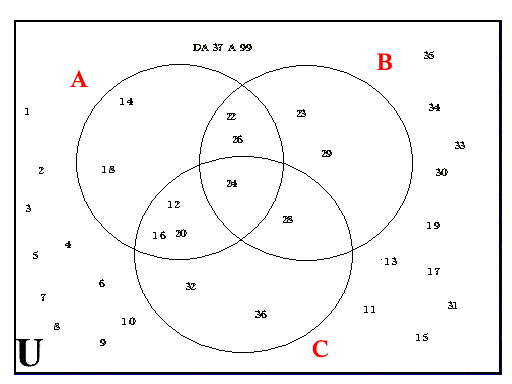
A = {12, 14, 16, 18, 20, 22, 24, 26}

Nell’espressione B = , l’elemento incognito indica tutti quei numeri compresi tra 20 e 30, escludendo i due sopra citati.
Il risultato della semplificazione dell’espressione in questione sarà:

B={21, 22, 23, 24, 25, 26, 27, 28, 29}

C={12, 16, 20, 24, 28, 32, 36}

L’espressione C è già semplificata.

U =

Sapendo infine che nell’espressione l’elemento incognito è minore di 100 ed esclude tutti i numeri già presenti nelle espressioni precedentemente semplificate.
Dall’insieme di queste espressioni si avrà la seguente rappresentazione grafica:

L'espressionesi semplifica utilizzando le leggi di De Morgan:
Sapendo che il simbolo (e non “U”) indica l’unione; che il simbolo indica l’intersezione e che il simbolo indica la negazione(o complementarietà) degli elementi, si agirà dividendo in varie parti l’espressione e si partirà dalla negazione più alta; individuato il punto, si spezzerà e si risolverà cambiando il simbolo interessato:

diventa

A questo punto, avendo due negazioni uguali una sotto l'altra, non possiamo spezzare ulteriormente; si semplifica (come accade sempre in presenza di due negazioni poste sullo stesso elemento).
Sarà:

diventa

La rappresentazione grafica di queste espressioni sarà quindi:

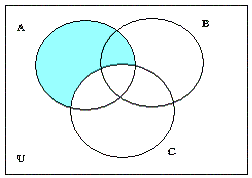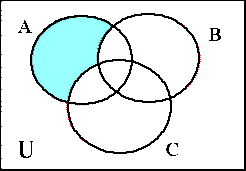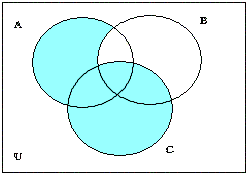Mettendo in relazione i risultati delle rappresentazioni precedenti con il risultato dell’ultimo enunciato rappresentato, si avrà:

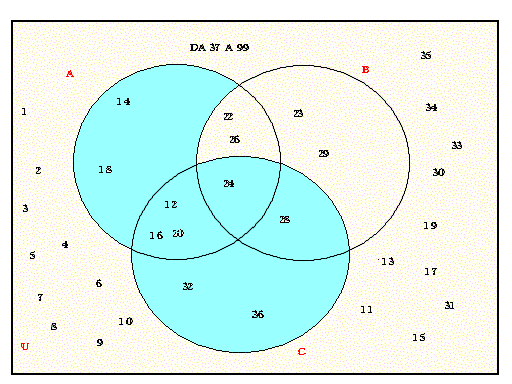
Quindi l’insieme D risulterà il seguente:

D = {12, 14, 16, 18, 20, 24, 28, 32, 36}