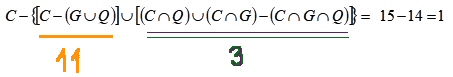PROBLEMA CON INSIEMI
Consideriamo il seguente problema
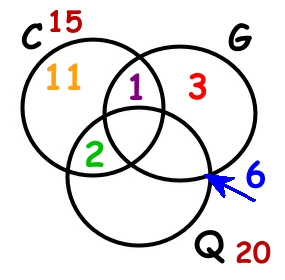
In un condominio vivono 35 famiglie. Tutti posseggono almeno un cane o un gatto o un quadro. 3 famiglie hanno solo dei gatti; 6 posseggono almeno un gatto e un quadro; 2 famiglie posseggono sia dei quadri che dei cani ma nessun gatto; 20 posseggono almeno dei quadri; 15 famiglie posseggono almeno un cane; 1 famiglia possiede sia un cane che un gatto ma nessun quadro; 11 famiglie posseggono solo dei cani
Quante sono le famiglie che posseggono almeno un gatto?
Quante sono le famiglie che posseggono solo dei quadri?
Quante sono le famiglie che posseggono sia un cane che un gatto che un quadro?
Il procedimento risolutivo è composto da tre passi:
1_ costruire il diagramma di Venn relativo ai dati
2_ rappresentare i dati in forma insiemistica
3_ rispondere ai quesiti in forma insiemistica
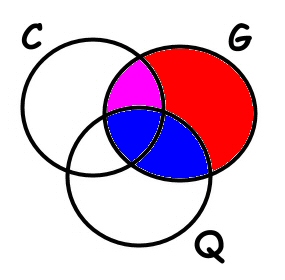
PRIMO PASSO: Iniziamo, dopo aver letto attentamente tutto il testo, con l’osservare che gli insiemi presi in considerazione sono tre: Cani (C), Gatti (G), Quadri (Q)
Passiamo quindi ad inserire i dati leggendo attentamente il testo.
La prima informazione che viene data è che tutti posseggono qualcosa quindi l’universo (U) coincide con l’unione di C, G, Q ovvero U= 
= 35
Quindi andando in sequenza
SECONDO PASSO
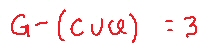oppure più preciso,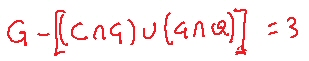 
,
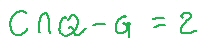oppure, più preciso, 
,
,
, 
,
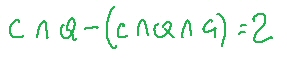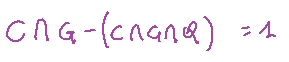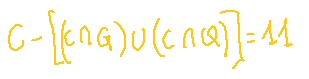
TERZO PASSO
Passiamo ora alla soluzione dei quesiti
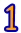Quante sono le famiglie che posseggono almeno un gatto?
Le famiglie che posseggono almeno un gatto (ma nulla vieta che qualcuno possa avere anche cani o quadri), ovvero G si ottengono unendo la parte blu, viola e rossa
ovvero
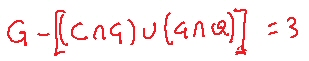unito
unito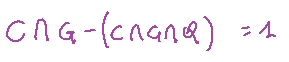
quindi 
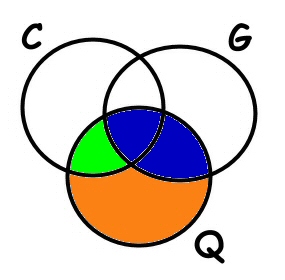
Quante sono le famiglie che posseggono solo dei quadri?
Le famiglie che posseggono solo dei quadri sono tutte quelle che posseggono dei quadri meno quelle che posseggono sia quadri che cani e quelle che posseggono sia quadri che gatti
ovvero 
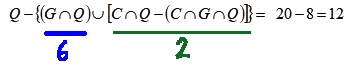
Quante sono le famiglie che posseggono sia un cane che un gatto che un quadro?
Le famiglie che posseggono contemporaneamente cani, gatti e quadri sono
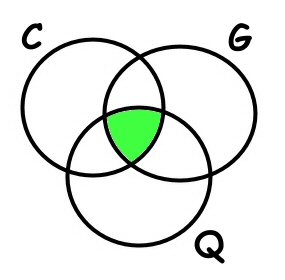
che possiamo ottenere partendo da C
ovvero 