DISQUAZIONE ESPONENZIALE

Partiamo dal testo della disequazione

e come primo passo scomponiamo le potenze

ora possiamo porre e andando a sostituire otterremo

a questo punto risolviamo la disequazione di secondo grado spuria con il metodo del raccoglimento (annullamento del prodotto)

che si annulla per e

quindi analizziamo le soluzioni o con il metodo della parabola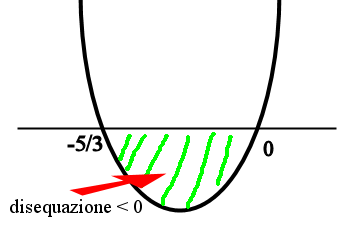

oppure con il metodo tradizionale del prodotto dei segni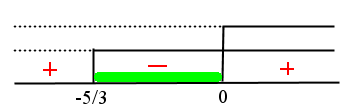

consideriamo l'intervallo interno (disequazione < 0). Di conseguenza consideriamo i casi

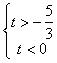e risostituendo la variabile t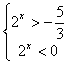

la seconda disequazione è impossibile in quanto l’esponenziale è sempre maggiore di 0

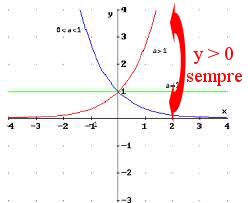
la prima può essere risolta tramite la definizione di logaritmo ovvero applicando il logaritmo sia a destra che a sinistra dell’operatore di disequazione ottenendo però per il secondo termine che risulta impossibile in quanto l’argomento del logaritmo (x) deve essere sempre maggiore di 0

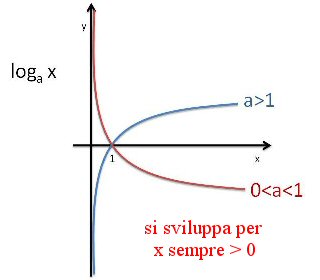
ne consegue che la disequazione di partenza non è soddisfatta per nessun valore di x(non esiste alcun vaore di x nel campo reale)