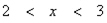DISEQUAZIONE ESPONENZIALE
Prendiamo in considerazione il seguente testo
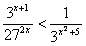
possiamo notare che si tratta di una disequazione esponenziale frazionaria.
Trasferiamo il termine a destra del simbolo di disequazione a sinistra
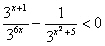
e successivamente fecciamo il mcm
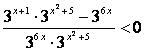
Ora risolviamo separatamente il numeratore e il denominatore, come in tutte le disequazioni frazionarie
N)
Poniamo il numeratore maggiore di zero
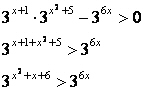
essendo presente sia a destra che a sinistra del simbolo di disequazione la stessa base, possiamo considerare solo gli esponenti
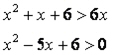
che risolvendo dà
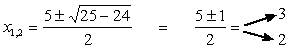
e quindi, dal grafico delle soluzioni
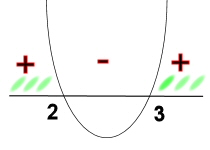
si deriva che la soluzione del numeratore è data dai valori esterni 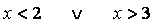
D)
Poniamo il denominatore maggiore di zero
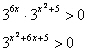
osservando che l'esponenziale è per definizione maggiore di zero si deduce che la disequazione è sempre soddisfatta. Quindi per il denominatore scriveremo 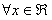
Analizzando le soluzioni del numeratore e del denominatore per mezzo del grafico delle soluzioni
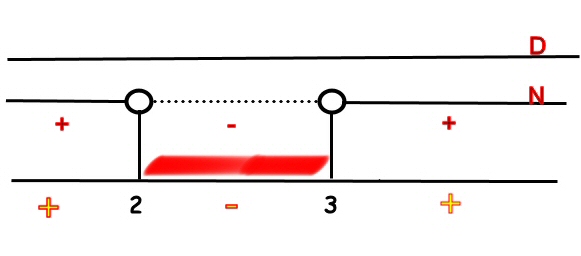
si ottiene, ricordando che il verso della disequazione era minore di zero, l'insieme dei valori compresi tra 2 e 3, ovvero