EQUAZIONI GONIOMETRICHE
elementari
Ricordiamo che una equazione si dice goniometrica se almeno una funzione goniometrica ha nel suo argomento una incognita.
Vediamo alcuni esempi di equazioni goniometriche elementari:
1_ Troviamo il valore dell'angolo ![]() per cui
per cui ![]()
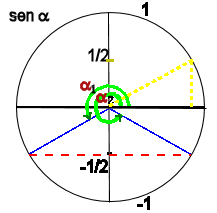 partendo dalla circonferenza goniometrica possiamo osservare che il valore del seno cercato si trova nella parte negativa dell'asse y.
partendo dalla circonferenza goniometrica possiamo osservare che il valore del seno cercato si trova nella parte negativa dell'asse y.
Allo stesso valore corrispondono due angoli (tratteggio rosso).
Il seno corrispondente a questi due angoli corrisponde, cambiato di segno, al seno di un particolare angolo situato nel primo quadrante (in giallo).
Ovvero ![]() e
e ![]() hanno lo stesso seno di
hanno lo stesso seno di ![]()
quindi abbiamo le due soluzioni:
![]() e
e ![]()
![]() indica (con k=0,1,2,3,...) che la funzione seno ha lo stesso valore dopo
indica (con k=0,1,2,3,...) che la funzione seno ha lo stesso valore dopo ![]() , 2
, 2![]() , 3
, 3![]() , ecc. (questo perché ha un periodo di
, ecc. (questo perché ha un periodo di ![]() )
)
2_ Troviamo il valore dell'angolo ![]() per cui
per cui ![]()
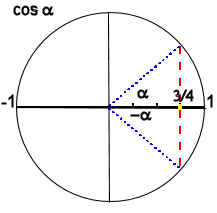
partendo dalla circonferenza goniometrica possiamo osservare che il valore del coseno cercato si trova nella parte positiva dell'asse x.
Allo stesso valore corrispondono due angoli (![]() e -
e -![]() ).
).
Il coseno corrispondente a questi due angoli non corrisponde al coseno di un angolo particolare, quindi per poter trovare l'angolo corrispondente facciamo ricorso alla funzione inversa del coseno.
quindi abbiamo due soluzioni coincidenti (in quanto ![]() )
)
quindo la soluzione coincidente è
![]()
anche per il coseno ![]() indica (con k=0,1,2,3,...) che la funzione coseno ha lo stesso valore dopo
indica (con k=0,1,2,3,...) che la funzione coseno ha lo stesso valore dopo ![]() , 2
, 2![]() , 3
, 3![]() , ecc. (questo perché ha un periodo di
, ecc. (questo perché ha un periodo di ![]() )
)
3_ Troviamo il valore di ![]() per cui
per cui ![]()
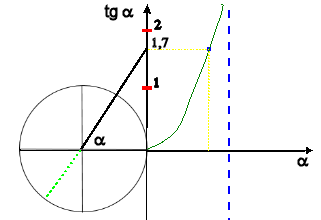
partendo dalla circonferenza goniometrica possiamo osservare che il valore della tangente cercato si trova nella parte positiva dell'asse y.
Consideriamo il fatto che ![]() quindi nel cercare il valore dell'angolo possiamo osservare che questo è un angolo particolare.
quindi nel cercare il valore dell'angolo possiamo osservare che questo è un angolo particolare.
Un'altra cosa da tenere in considerazione è che la tangente ha un periodo di ![]() .
.
Da tutto ciò discende che la soluzione cercata è
![]()
