GRAFICI DI FUNZIONI E DOMINIO

Nello studio delle funzioni matematiche abbiamo affrontato, per ora tre tipologie.

La prima tipologia è caratterizzata dall’avere una espressione in cui compare una sola x e con l’esponente 1.

La rappresentazione grafica è quella di una retta.

Esempi di funzioni di questa prima tipologia sono:

$y=\frac{2}{3}x-2$

$y=x+2$

$y=-3x-1$

$y=x$

$y=x-\frac{1}{2}$

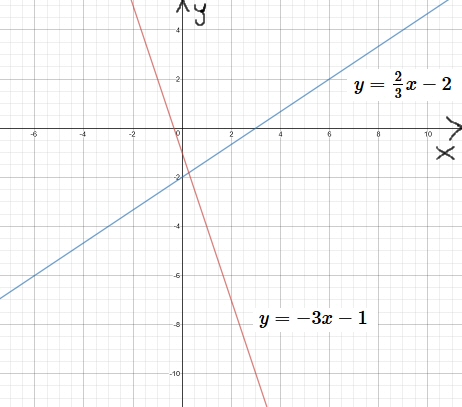
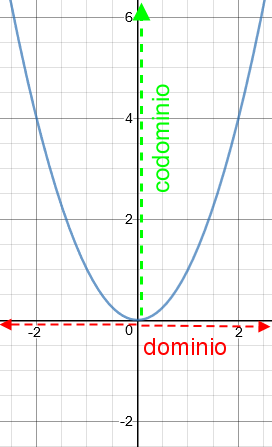
In questa tipologia di funzione il Dominio (Campo di Esistenza) della x è dato da tutti i valori reali, quindi possiamo scrivere

C.E. =  $\mathrm{\forall }x\in R$

(quindi alla x possono essere assegnati tutti gli infiniti valori da meno infinito $-\mathrm{\infty }$ a più infinito $+\mathrm{\infty }$)

Lo stesso possiamo dire del Codominio $\mathrm{\forall }y\in R$

(quindi alla y possono essere assegnati tutti gli infiniti valori da meno infinito $-\mathrm{\infty }$ a più infinito $+\mathrm{\infty }$)

La seconda tipologia è caratterizzata dall’avere un’espressione in cui compare almeno una x con esponente 2.

La rappresentazione grafica è quella di una parabola.

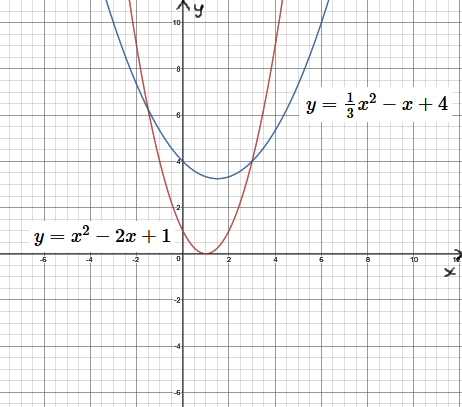
Esempi di funzioni di questa seconda tipologia sono:

$y=3x^2-2x$

$y=-x^2+3x$

$y=x^2-2x+1$

$y=\frac{1}{3}{x}^2-x+4$

$y=x^2$

$y=x^2+\frac{3}{2}$

In questa tipologia di funzione il Dominio (Campo di Esistenza) della x è dato da tutti i valori reali, quindi possiamo scrivere

C.E. =  $\mathrm{\forall }x\in R$

(quindi alla x possono essere assegnati tutti gli infiniti valori da meno infinito $-\mathrm{\infty }$ a più infinito $+\mathrm{\infty }$)

Non lo stesso possiamo dire del Codominio.

Infatti nel caso $y=x^2$ il Codominio sarà dato da $\mathrm{\forall }y>0$

(quindi alla y possono essere assegnati tutti gli infiniti valori da zero 0 a più infinito $+\mathrm{\infty }$)

mentre per l’espressione $y=-x^2+\frac{3}{2}$ il Codominio sarà $\mathrm{\forall }y<\frac{3}{2}$

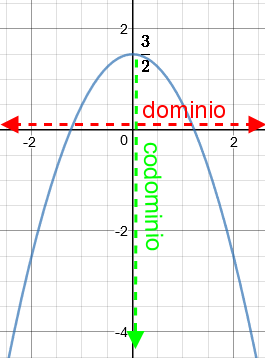
(quindi alla y possono essere assegnati tutti gli infiniti valori da tre mezzi $\frac{3}{2}$ a meno infinito $-\mathrm{\infty }$)

La terza tipologia è caratterizzata dall’avere un’espressione in cui compare almeno una x a denominatore. Nelle sue espressioni più semplici la x che si trova a denominatore ha esponente 1.

La rappresentazione grafica richiama quella di una iperbole.

Esempi di funzioni di questa terza tipologia sono:

$y=\frac{2}{(2x+3)}$

$y=\frac{1}{(2x+3)(x-1)}$

 $y=\frac{2x}{(\frac{3}{5}x+1)}$

$y=\frac{1}{x}$

$y=-\frac{1}{x}$

$y=-\frac{1}{x(2-x)}$

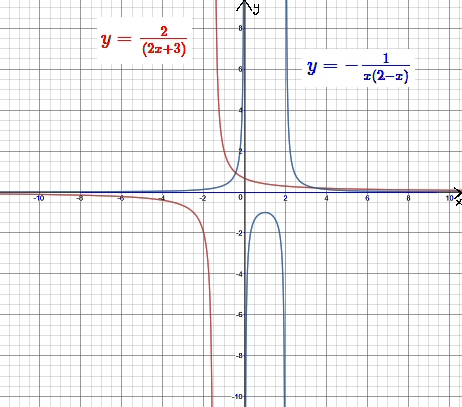
In questa tipologia di funzione il Dominio (Campo di Esistenza) della x potrebbe non essere dato da tutti i valori reali. Infatti la presenza della x a denominatore può determinare il caso in cui il denominatore si annulli. Questa eventualità deve essere esclusa dato che il denominatore di una frazione non può mai essere nullo.

Affinché l'espressione rispetti la definizione di funzione dobbiamo quindi restringere il Dominio escludendo da tutti i valori reali $R$ quelli che rendono nullo il denominatore.

Primo esempio

Nel caso $y=\frac{2}{(2x+3)}$ la x non potrà assumere il valore $-\frac{3}{2}$ perché questo valore renderebbe nullo il denominatore. Infatti

$2(-\frac{3}{2})+3=0$ e la funzione risulterebbe $y=\frac{2}{0}$ e quindi impossibile.

Quindi, in questo caso, il Dominio (Campo di Esistenza) della x sarà

C.E. =  $\mathrm{\forall }x\in R-\{-\frac{3}{2}\}$

Secondo esempio

Nel caso $y=\frac{1}{(2x+3)(x-1)}$ la x non potrà assumere né il valore $-\frac{3}{2}$ né il valore di 1 perché questi valori renderebbero nullo il denominatore. Infatti

$2(-\frac{3}{2})+3=0$ e $1-1=0$ e la funzione risulterebbe in entrambe i casi  $y=\frac{1}{0}$ e quindi impossibile.

Quindi, in questo caso, il Dominio (Campo di Esistenza) della x sarà

C.E. =  $\mathrm{\forall }x\in R-\{-\frac{3}{2},1\}$

Per trovare il o i valori che vanno esclusi si può procedere in uno dei seguenti modi:

1_

pongo ogni denominatore uguale a zero e ricavo la x come fosse una equazione

esempio: $y=\frac{2}{(2x+3)}$ pongo $2x+3=0$ e ricavo la x come in una equazione => $x=-\frac{3}{2}$

2_

considero il denominatore della funzione

esempio: $y=\frac{2}{(2x+\frac{3}{5})}$

di questa funzione il denominatore è $2x+\frac{3}{5}$

quindi procedo nel seguente modo: dato che per annullare il denominatore dovrò trovare un valore che moltiplicato per 2 dovrà darmi $\frac{3}{5}$ cambiato di segno inizio con l'assegnare alla x il valore $\frac{3}{5}$ cambiato di segno, ovvero $-\frac{3}{5}$.

Quindi dato che c'è un 2 a moltiplicare la x dovrò fare in modo che sparisca dividendo per il due stesso.

Quindi divido il valore assegnato alla x, $-\frac{3}{5}$, per 2 ovvero $-\frac{\frac{3}{5}}{2}$ = $-\frac{3}{5\cdot 2}$ = $-\frac{3}{10}$

Avremo così C.E. =  $\mathrm{\forall }x\in R-\{-\frac{3}{10}\}$

Se i termini contenenti la x a denominatore sono più di uno si applica più volte uno dei due procedimenti illustrati.

Per come realizzare il grafico vedi Grafico di funzione e Grafico di funzione 1