GRAFICO DI FUNZIONE

Si vuole tracciare il grafico della funzione

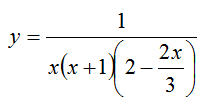
Per prima cosa bisogna trovare il campo di esistenza della funzione. Dato che si tratta di una funzione con la x a denominatore, vado a vedere quando il denominatore si annulla.
I valori che annullano il denominatore sono i valori da togliere dall’insieme dei reali questo caso il Campo di Esistenza è .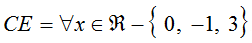

Per trovare i valori cerco i valori che annullano i singoli elementi del denominatore, ovvero:

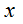  => x = 0

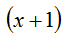=> x = -1

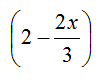=> x = 3 (in questo modo sostituendo 3 ad x ottengo )

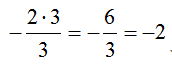A questo punto osserviamo che i tre valori che annullano il denominatore rappresentano anche tre asintoti a cui tende la funzione. Ricordiamo che un asintoto è una retta alla quale si avvicina indefinitamente una funzione data, cioè una retta alla quale una curva si avvicina senza mai raggiungerla.

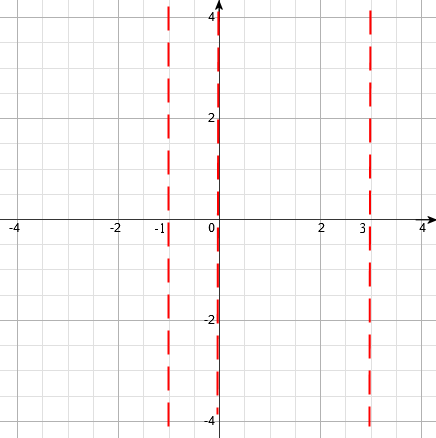
Dopo aver tracciato gli asintoti, assegniamo alcuni valori alla x e calcoliamo i corrispondenti valori di y. Per fare questo costruiamo una tabella per ogni zona in cui è diviso il piano cartesiano dagli asintoti (ovvero quattro zone).

Assegnamo alcuni valori alla x

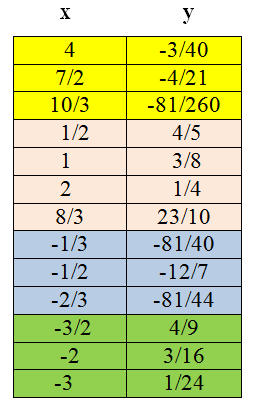 e di conseguenza tracciamo il grafico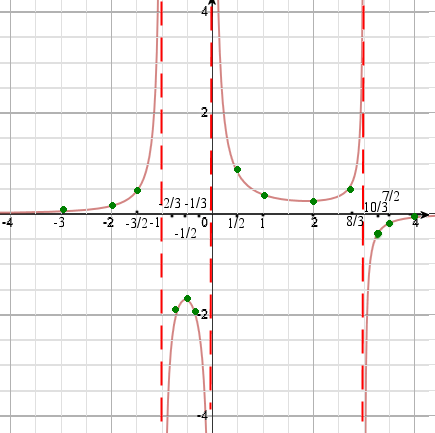

vedi anche Grafici di funzioni e dominio o Grafico di funzione