GRAFICO DI FUNZIONE
Si vuole tracciare il grafico della funzione
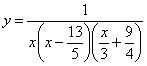
Per cominciare si guarda di che grado è l’espressione per avere un’idea del grafico. Esempio:se è di 1° grado è una retta, se è di 2° grado è una parabola ecc. In questo caso è di 3° grado.
Successivamente si trova il campo di esistenza. Il campo di esistenza (CE) o dominio naturale è l’insieme dei numeri che attribuiti alla variabile indipendente (cioè alla x) definiscono la funzione. Le funzioni razionali intere sono definite in tutto l’asse quindi il dominio si estende all’infinito. Mentre le funzioni razionali fratte, come in questo caso, sono definite da tutti i valori che non annullano il denominatore.
Quindi in questo caso il CE è dato da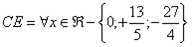 
(dove 
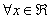= per ogni x appartenente al insieme dei numeri reali).
Vediamo perché.
Nella nostra funzione se al posto della x mettiamo 0, il denominatore si annulla perché qualsiasi numero moltiplicato per 0 è uguale a 0 quindi l’espressione diventerebbe impossibile.
Se sostituissimo alla x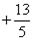
nuovamente il denominatore si annullerebbe perché è l’opposto di 
.
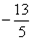Infine osservando 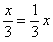che 
e che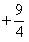 
è l'opposto di 
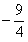si ha xhe l'ultimo valore che annulla il denominatore è dato da 
.
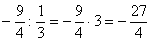A questo punto osserviamo che i tre valori che annullano il denominatore rappresentano anche tre asintoti a cui tende la funzione. Un asintoto è una retta alla quale si avvicina indefinitamente una funzione data, cioè una retta alla quale una curva si avvicina senza mai raggiungerla.
Dopo aver tracciato gli asintoti viene costruita la tabella per punti della funzione, ovvero vengono attribuiti dei valori alla x per trovare la y corrispondente calcolando così l’espressione numerica e trovando le coordinate cartesiane che si intersecano in un punto. Visto che ci sono tre asintoti, ci sono allora quattro zone e per ogni zona viene costruita una tabella.
Assegnamo alcuni valori alla x
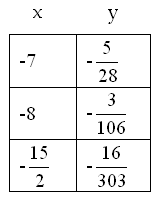
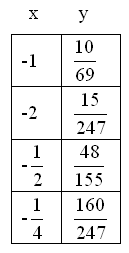
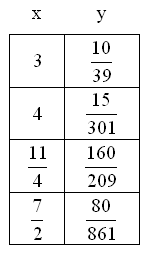
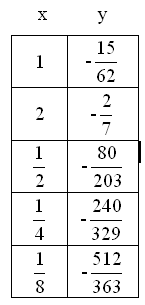
il grafico corrispondente è
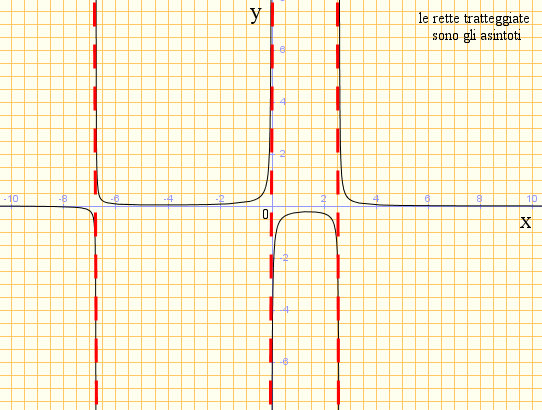
vedi anche Grafici di funzioni e dominio o Grafico di funzione 1